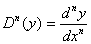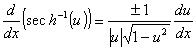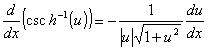Material de apoio - (calculo - derivadas)
Derivadas
| A derivada de uma função y = f(x) num ponto x = x0 , é igual ao valor da tangente trigonométrica do ângulo formado pela tangente geométrica à curva representativa de y=f(x), no ponto x = x0, ou seja, a derivada é o coeficiente angular da reta tangente ao gráfico da função no ponto x0. |
A derivada de uma função y = f(x), pode ser representada também pelos símbolos:
y' , dy/dx ou f ' (x).
A derivada de uma função f(x) no ponto x0 é dada por:
![]()
Algumas derivadas básicas
Nas fórmulas abaixo, u e v são funções da variável x.
a, b, c e n são constantes.
Derivada de uma constante
![]()
Derivada da potência
![]()
Portanto:
![]()
Soma / Subtração
![]()
Produto por uma constante
![]()
Derivada do produto
![]()
Derivada da divisão
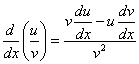
Potência de uma função
![]()
Derivada de uma função composta
![]()
Derivadas
Regra da cadeia
A fórmula:
![]()
é conhecida como regra da cadeia. Ela pode ser escrita como:
![]()
Outra fórmula similar é a seguinte:
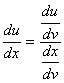
Derivada da função inversa
A inversa da função y(x) é a função x(y):
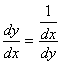
Derivadas de funções trigonométricas e suas inversas
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
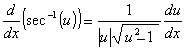
![]()
Derivadas de funções exponencial e logarítmica
Derivada do logaritmo natural
![]()
Derivada do logaritmo
em outras bases
![]()
Exponencial
![]()
![]()
![]()
Lembre-se da definição da função logarítmica com base a > 0:
![]()
Derivadas das funções hiperbólicas e suas inversas
Lembre-se das definições das funções trigonométricas:
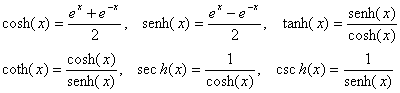
Derivadas de alta ordem
Seja y = f(x). Temos:
A segunda derivada é dada por:
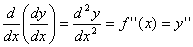
A terceira derivada é dada por:
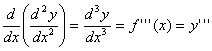
A enésima derivada é dada por:
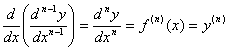
Em alguns livros, a seguinte notação também é usada: